Generating 2D random fractal terrains with C#

Back in 1999, when I was learning C++ and MFC, I remember spending a great deal of time writing an application that displayed the Mandelbrot set, probably the most famous of all fractals. And when I learned Remote Procedure Call, I even converted the application into a distributed Mandelbrot generator (which made sense given the CPU speed of the time).

What’s so fascinating about the Mandelbrot set, and other fractals, is that the often simple equations that define them are able to give birth to such complex creations.

In general, a fractal is defined as:

“[…] ‘a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole,’ a property called self-similarity. A fractal often has the following features: it has a fine structure at arbitrarily small scales; it is too irregular to be easily described in traditional Euclidean geometric language; it is self-similar (at least approximately or stochastically); [… and] it has a simple and recursive definition. […] Natural objects that approximate fractals to a degree include clouds, mountain ranges, lightning bolts, coastlines, and snowflakes.”

The Mandelbrot set is an example of a fractal whose definition contains no stochastic element, i.e., the fractal looks the same every time it’s generated. Recently, though, I came across a simple algorithm that claimed to generate fractal terrains by adding randomness to the equation. So, given my history with fractals, I wanted to play with the algorithm that’s based on progressive refinement through midpoint displacement in one dimension:

Start with a single horizontal line segment
Repeat for a sufficiently large number of times
    Repeat over each line segment
        Find the midpoint of the line segment
        Displace the midpoint in y by a random amount
    Reduce the range for random numbers

Here’s my implementation of the algorithm in C#:

using System;
using System.Collections.Generic;

namespace FractalTerrain {
    class Point {
        public double x;
        public double y;
    }

    class Program {
        static void Main(string[] args) {
            int iterations = 8;
            double roughness = 0.5;
            double displacementFactor = 1.0;
            Random generator = new Random();
            double[] ys = { 0.0, 0.0 };

            for (int i = 0; i < iterations; i++) {
                ys = Split(ys, displacementFactor, generator);
                displacementFactor *= roughness;
            }

            Point[] points = ComposeCoordinatePairs(ys);
            foreach (Point p in points) {
                Console.WriteLine("{0:0.000} {1:0.000}", p.x, p.y);
            }
        }

        static double[] Split(double[] ys, double displacementFactor, Random generator) {
            double[] newYs = new double[2 * ys.Length - 1];

            for (int i = 0; i < ys.Length - 1; i++) {
                double midpoint = (ys[i] + ys[i + 1]) / 2.0;
                double displacement = generator.NextDouble() * displacementFactor;
                newYs[2 * i] = ys[i];
                newYs[2 * i + 1] = midpoint + displacement;
            }

            return newYs;
        }

        static Point[] ComposeCoordinatePairs(double[] ys) {
            double increment = 1.0 / (ys.Length - 1);
            Point[] points = new Point[ys.Length];

            for (int i = 0; i < ys.Length; i++) {
                points[i] = new Point();
                points[i].x = increment * i;
                points[i].y = ys[i];
            }

            return points;
        }
    }
}

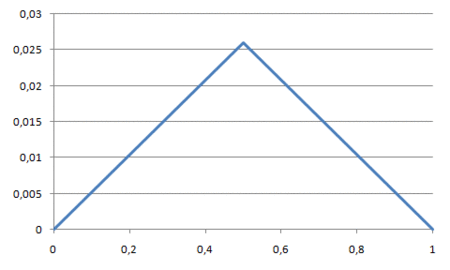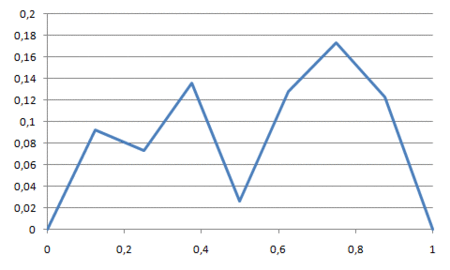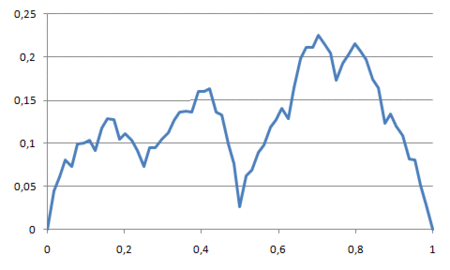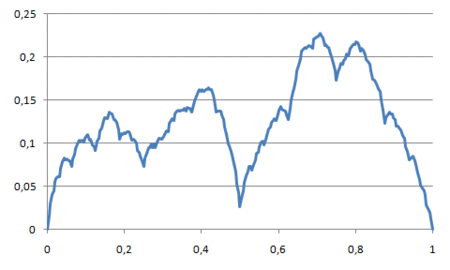
Splitting line segments, the C# code doesn't store the x-component of the coordinate pairs because it can be inferred from the number of y-components and the fact that x-components go from 0 to 1, both inclusive. Hence, starting with the line segment (0,0)-(1,0), the code splits it by calling the Split method passing in a list of y-components of the line segment. After the first iteration the single line segment becomes two, then four, then eight, and so on until the line segments have undergone eight iterations of splitting. Generally, after the i'th iteration the number of line segments is 2^i and so after eight iterations we end with 256 line segments.

As prescribed by the algorithm, merely splitting line segments doesn’t give rise to a mountain. The mountain emerges because each time a line segment is split in two, a random displacement is added to the y-component at the center of the line segment. Assigning an upper limit to the maximum displacement within an iteration is what defines the roughness of the generated terrain. For the above implementation, the maximum displacement is defined as half of that of the previous iteration starting with 0.5. Thus, the first couple of iterations roughly define the terrain and additional iterations fill in the details.

In animated form the transformations from two to 256 line segments looks like so:

Among the practical applications of such a random fractal terrain generator are computer games. Not necessarily for generating 2D ridgelines, but for generating entire 3D terrains or even clouds. It works by generalizing 1D midpoint displacement to 2D in the form of the diamond-square algorithm. Then a cloud, for instance, can be derived from the 3D terrain by applying a height map to it; a height map in which different heights get assigned different colors.