Trustpilot challenge: dictionary-based multi-word anagram solver with a twist

Following the previous Trustpilot challenge of cracking an AES encrypted message, a new job ad challenge is up:

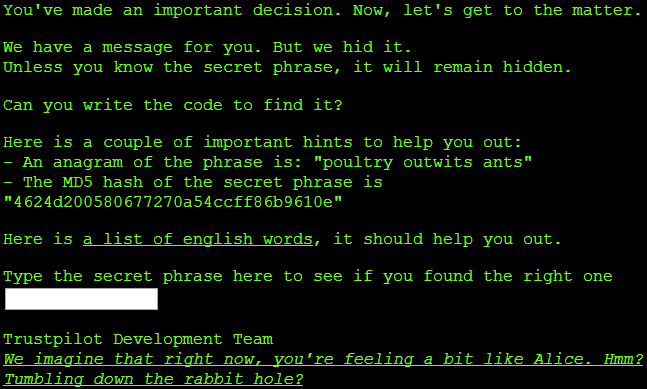
This challenge proved much harder than the previous. With an 18 character anagram, a brute-force approach would require trying out 18! or 6,402,373,705,728,000 permutations of the letters (not counting anagrams with spaces). This is clearly an intractable approach, which is why Trustpilot provides a dictionary of 99,174 words to construct anagrams from.

To construct anagrams from a dictionary, I went with a recursive backtracking algorithm. It builds up a decision tree of dictionary words, recursively following branches for as long as valid anagram can be constructed from these (effectively trying out every valid permutation of words from the dictionary), otherwise it backtracks.

Given the dictionary of 99,174 words, the problem is still intractable. We can't simplify it further by including knowledge about md5 because its output is uniformly distributed. Our only choice is to further reduce the size of the dictionary before starting the construction of the decision tree. This can be done through histogram analysis as carried out by the F# functions below (see inline comments):

namespace TrustpilotChallenge

[<AutoOpen>]
module Anagram =
    // when two words are anagrams of each other, their alphabetized forms 
    // are equal, i.e., their letter histograms are equal
    let letterHistogram anagram =
        // get rid of spaces as they get inserted by the anagram solver
        // between each word from the dictionary, i.e., the number of
        // spaces in different anagrams is unimportant.
        anagram
        |> Seq.toList
        |> Seq.filter (fun c -> c <> ' ')
        |> Seq.groupBy (fun c -> c) 
        |> Map.ofSeq
        |> Map.map (fun k v -> Seq.length v)

    // subtracts letter histograms of two words if every frequency 
    // remains positive after the subtraction. The result is a 
    // new histogram of positive frequencies
    let inline subtractHistograms (h1: Map<char, int>) (h2: Map<char, int>) =
        let sharedAlphabet = h2 |> Map.forall (fun k _ -> h1.ContainsKey k)
        if sharedAlphabet then
            let diff =
                h1 |> Map.map (fun w h -> 
                    match h2.TryFind w with
                    | Some value -> h - value
                    | None -> h)
            let positives = diff |> Map.forall (fun w h -> h >= 0)
            if positives then Some (diff |> Map.filter (fun _ h -> h > 0))
            else None
        else None

    // only include dictionary words which has <= same count 
    // of individual letters as the anagram
    let pruneWords anagram wordLetterHistograms =
        let h1 = letterHistogram anagram
        wordLetterHistograms
        |> Seq.filter (fun (_, h2) -> 
            subtractHistograms h1 h2 |> Option.isSome)

    let createWordLetterHistograms dictionary =
        dictionary |> Seq.map (fun w -> (w, letterHistogram w)) 

    let findAnagrams wordLetterHistograms anagram =
        let rec findAnagram' histogram wordsSoFar =
            seq {
                for (w, h2) in wordLetterHistograms do
                    match (subtractHistograms histogram h2) with
                    | Some h2 ->
                        if h2 |> Map.isEmpty 
                        then yield List.rev (w :: wordsSoFar)
                        else yield! findAnagram' h2 (w :: wordsSoFar)
                    | None -> () }

        findAnagram' (letterHistogram anagram) List.empty<string>

Removing duplicate words and pruning the dictionary using histogram analysis, we end up with a dictionary of 1,658 words. The reduced-size dictionary contains too many single and double letter words compared to what's allowed in the English language which "artificially" inflates the search space. In fact, assuming it's allowed to construct anagrams by reusing single letter words, the search space grows toward 18! permutations.

Single and double letter words or not, recursively constructing permutations of around 1,600 words and backtracking when the permutation is valid or invalid is still an intractable problem.

To make the problem tractable, we need to combine recursive backtracking with heuristics, such as looking for solutions constructed of longer words. Though it doesn't necessarily yield a solution that also satisfies the md5 property, it does reduce the search space significantly and makes exhaustive search possible:

[<AutoOpen>]
module Hashing =
    open System
    open System.Text
    open System.Security.Cryptography

    let inline md5FromString s =
        // the compiler prforms overload resolution of GetBytes
        // based on parameter name. Otherwise we'd have to add
        // a type annotation
        BitConverter
            .ToString(MD5
                .Create()
                .ComputeHash(Encoding.UTF8.GetBytes(s = s)))
            .Replace("-", "")

module Program =  
    open System
    open System.IO

    [<EntryPoint>]
    let main _ =  
        let path = "../../wordlist"
        let anagram = "poultry outwits ants"
        let md5outcome = "4624d200580677270a54ccff86b9610e".ToUpper()
        let dictionary = 
            File.ReadAllLines(path)
            |> Seq.distinct
            |> Seq.filter (fun w -> w.Length > 3)
            |> Seq.sortBy (fun w -> w.Length)
            |> createWordLetterHistograms
            |> pruneWords anagram
            |> Seq.toArray
            |> Array.rev

        // iterative approach
        for anagram in (findAnagrams dictionary anagram) do
            let anagram' = anagram |> List.reduce (fun acc w -> acc + " " + w)
            if md5FromString anagram' = md5outcome then
                printfn "Secret: %s" anagram'
                Environment.Exit(0)

        (* FP pipelining approach. Harder to debug than iterative one
        findAnagrams dictionary anagram
        |> Seq.map (fun a -> a |> List.reduce (fun acc w -> acc + " " + w))
        |> Seq.map (fun a -> (a, md5FromString a))
        |> Seq.filter (fun (_, md5) -> md5 = md5outcome)
        |> Seq.map (fun (w, _) -> w)
        |> Seq.truncate 1
        |> fun s -> printfn "Secret: %A" s *)    
        0

Perhaps adding heuristics to the equation makes for a less attractive solution. It certainly requires experimentation to come up with the right heuristics and not all heuristics are applicable to all anagrams. In the end, recursive backtracking and heuristics yield a solution in less than 30 seconds of running time.